"The NY Math Briefs are critically flawed"

A guest post by Professor Benjamin Solomon on the multiple omissions and inaccuracies in the newly released NY math briefs and why they should be withdrawn

Today I am sharing a guest post by

Benjamin

, an Associate Professor in School Psychology at the University of Albany, about what is wrong with the recently released New York math briefs and why NYSED should withdraw them.

Below is a letter that Professor Solomon and others wrote to Commissioner Rosa.

You can find the original letter with all the footnotes here.

You can sign their petition to withdraw the Math Briefs here.

You can listen to his podcast with mathematician Dr. Anna Stokke talking about this issue here.

Dear Commissioner Rosa,

We, a diverse group of both local and international educational leaders, educators, and researchers, were initially pleased to learn of New York’s new math initiative. Math proficiency is the entry point to vocational and post-secondary career opportunities and enables a healthy thriving workforce that fuels the economy of our state. We bear the moral responsibility to equip all children with mathematical knowledge to give them access to their future lives. By promoting research-based teaching methods, we can close opportunity gaps in student achievement while raising achievement for all students and ensuring the competitive vitality of our state for the businesses of the future.

It is deeply concerning, however, that the recently released New York math briefs are critically flawed. This letter outlines serious concerns regarding grave omissions and inaccuracies in the New York math briefs in summarizing what’s purported to be evidence-based math instruction. Given the detrimental impact on New York’s youth, we are calling for a retraction of the New York math briefs. We request that they be replaced with materials that are accurate and based on evidence from rigorous empirical studies. Given recent national attention to student literacy, we are concerned that the briefs inexplicably reinforce several of the exact myths dispelled in the Science of Reading.

Omitted findings include the results of rigorous empirical studies, such as those funded through competitive federal grant competitions. Conclusions from these experimental studies, including randomized control trials, are public and synthesized in a series of What Works Clearinghouse best practice guides, the National Mathematics Advisory Panel and Project Follow Through. The recommendations also conflict with extant published NYSED guidance and policy, in addition to nationally recognized action and policy non-profit centers, such as the National Center for Intensive Intervention and the IRIS center. Oddly, the briefs give passing reference to the What Works Clearinghouse (Briefs 7 and 8) and the National Center for Intensive Intervention (Brief 8) without enumerating on how recommendations from those works conflict with recommendations in the briefs.

Despite the conspicuous use of the word “science,” the briefs collectively cite only 2 experimental studies and 2 meta-analyses. Where peer-reviewed research is cited, it is overwhelmingly articles reflecting personal experiences and opinions (i.e., not experimental). There is an enormous body of rigorous randomized control trials and single-case experimental studies which converge on evidence-based instructional

strategies for teaching math which are overlooked in the briefs. For example, Powell and colleagues identified 9 rigorous peer-reviewed meta-analyses, encompassing hundreds of peer-reviewed studies, focused on students at-risk for math difficulties, which unfortunately is most students in this country.

Factual inaccuracies in the New York Math briefs

Factual inaccuracies in the briefs are shockingly abundant. We select the most prominent errors to expand upon below.

● The myth of math anxiety and timed testing being a cause of math anxiety (Brief 2). Research shows that brief timed tests do not cause math anxiety (Binder, 1996; Codding et al., 2023). In fact, these brief assessments, commonly falling under the umbrella of curriculum-based measurement, are the basis for universal academic screening (unmentioned in brief 5, assessment, and briefly mentioned without context in brief 8) which is required in most states as it allows schools to identify patterns of risk and individual student risk to facilitate mid-course instructional corrections at the program and individual to prevent academic failure. Advising teachers to minimize the use of brief timed tests is entirely antithetical to Response to Intervention and Multi-Tiered Systems of Support (MTSS). A MTSS pilot project has been thriving in NY for nearly five years and Response to Intervention is mandated in New York.

● The myth of explicit instruction (or direct instruction) being a selective instructional strategy, mostly useful for the disabled (Brief 2, 4, 7). A definition of explicit instruction is, “a group of research-supported instructional behaviors used to design and deliver instruction that provides needed supports for successful learning through clarity of language and purpose, and reduction of cognitive load. It promotes active student engagement by requiring frequent and varied responses followed by appropriate affirmative and corrective feedback and assists long-term retention through use of purposeful practice strategies.” (p. 143; Hughes et al., 2017). Abundant research has shown explicit instruction is vital for all students to acquire basic skills and must be used in abundance when teaching new material and skills (VanDerHeyden et al., 2012; Fuchs et al., 2012; 2023, Clarke et al., 2015; Stockard et al., 2018; WWC practice guides). Contrary to the brief’s opinion that direct instruction (a synonym for explicit instruction) is for “empty vessels,” it has been shown highly effective in laboratory and classroom settings to promote efficient learning and reduce anxiety with difficult content (Stockard et al., 2018; WWC practice guides). It is the foundational teaching approach embodied by the Science of Reading (Petscher et al., 2020) and the caricature of it in the NY brief is stunning

given that it has been shown to produce the highest level of academic engagement among learners and the most rapid mastery of new concepts which then enables creative and generative problem solving (Johnson & Layng, 1992). What is critical to understand is that we have been here before. In reading, the philosophy driven tactics (whole language) that were promoted undermined the explicit teaching of reading in the same way. To make this same mistake in math is a travesty and will harm our students.

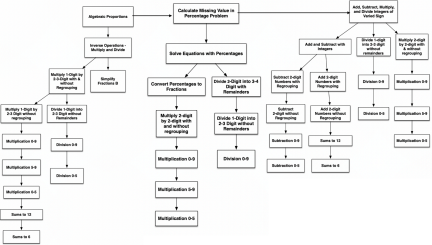
● The myth that structured repeated practice of math facts and standard algorithms isn’t useful (Brief 2, 3, Brief 7). Research has revealed the critical importance of being able to quickly recall both whole number math facts (e.g., subtraction from 18) and procedural problem-solving strategies (e.g., application of standard algorithm to 2x2 addition; solving for x; Fuchs et al., 2013; 2023; Hartman et a.l., 2023; McNeil et al, 2025; Stockard et al., 2018, VanDerHeyden et al., 2012; Rosenshine, 2012). These facts must be explicitly taught and students given ample structured practice such that they can demonstrate agile fact recall on timed assessments prior to generalizing concepts and skills to novel situations. A chronic problem with American curriculum is not that they overrepresent the practice of facts and algorithms (Brief 7), but that they offer far too little practice. All complex mathematical problem solving can be explained as the mastery of simpler operations and concepts. For example, one grade 8 expectation is solving algebraic proportions with a missing number in any position. This is endlessly useful to students in creating and converting quantities. Solving algebraic proportions cannot be learned if children have not mastered all the skills that are prerequisite, which paints a picture of the devastating cumulative effect of undermining early math mastery year over year (see figure below). The methods in the NY briefs diminish the critical importance of mastering and performing fluently or automatically all the foundational skills that build advanced math performance during primary and secondary education in math.

● The myth that discovery learning should be prioritized in early stages of acquisition (Brief 2, 4, 7). Discovery learning is discussed repeatedly but left undefined in the briefs. It is defined elsewhere as “an instructional method that encourages students to build their own understanding by exploring, manipulating, and experimenting, rather than being told or shown information directly” (Mayer, 2004). Discovery learning, often characterized as “applied” learning, exploration, or as experimentation is useful in building interest and connecting student’s foundational skills to real-world problems. However, it is likely only useful after students have demonstrated high levels of fluency on underlying skills (Hartman et al., 2023; Kirschner et al., 2006; WWC practice guides; McNeil et al., 2025). And interestingly, the claim of greater student interest, motivation, or engagement has not been experimentally supported, whereas children are typically highly engaged in explicit instruction. In fact, the defining feature of explicit instruction is a very high rate of opportunities to respond, meaning all students are eager and capable of responding accurately, with task difficulty advancing in tandem with measured learning gains. This is why “systematic instruction” is identified as a necessary ingredient of math instruction by the Institute for Educational Science 2009 practice guide, which is contradicted by the NY math briefs. Discovery learning is important, but it should occur for mastered concepts and skills according to the science of how humans learn, not when a new skill is being introduced as suggested by the NY briefs.

We are calling for a retraction of the New York math briefs. We urge that they be replaced with accurate materials informed by the most reliable evidence. We believe this is critical to improving math achievement amongst New York’s youth. The undersigned are happy to provide guidance or recommend others knowledgeable in this area. Our sole goal is for students in New York to receive sound evidence-based instruction so they can thrive into adulthood and support New York’s competitiveness in STEAM-related areas.

Respectfully,

- Signatories Attached

Dr. Benjamin Solomon is an associate professor of School Psychology at the University at Albany. His research areas include academic assessment and intervention, especially for math, research methods and statistics, and multi-tiered systems of support. He is a strong advocate for the use of evidence-based practice and the science of learning in schools. He sits on the advisory board for several technical assistance centers and peer-reviewed journals. He is the former director of New York’s Technical Assistance Center for Academics, which works closely with the state’s educational department to promote best practice in academic assessment and instruction for students with disabilities.